From Bioblast
Description
Gibbs energy G [J] is exergy which cannot be created internally (subscript i), but in contrast to internal-energy (diU/dt = 0) is not conserved but is dissipated (diG/dt < 0) in irreversible energy transformations at constant temperature and (barometric) pressure, T,p. Exergy is available as work in reversible energy transformations (100 % efficiency), and can be partially conserved when the exergonic transformation is coupled to an endergonic transformation.
Abbreviation: G [J]
Reference: Energy
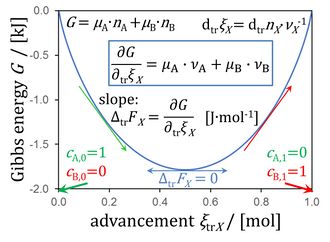
Figure 8.5. Gibbs energy as a function of advancement of a transformation (0 = -1 A + 1 B) in a closed isothermal system at constant pressure, for μA° = μB° = 0 kJ·mol-1 (modified from Gnaiger 2020 BEC MitoPathways - see Footnote 1).
Gibbs energy as a function of advancement
Communicated by Gnaiger E 2022-10-19
- In a transformation tr 0 = -1 A +1 B proceeding in a system with volume V at constant barometric pressure p, the Gibbs energy of reactants A and B is
Eq. 1: G = µA·nA + µB·nB [J]
- A small change dtrG at constant chemical potentials µi is due to a small advancement of a transformation tr, in closed or open isothermal systems, exchanging heat in equilibrium with an external thermostat at constant temperature,
Eq. 2: dtrG = µA·dtrnA + µB·dtrnB [J]
- where the advancement dtrξi (i = A or B) is
Eq. 3: dtrξi = dtrnA·νA-1 = dtrnB·νB-1 [mol]
- The total change of Gibbs energy dG is the sum of all partial transformations, dG = ΣdtriG, where tri = 1 to N transformation types — not to be confused with the internal Gibbs energy change diG due to internal transformations (i) only.
- The isomorphic force of transformation ΔtrFX is the derivative of exergy per advancement (Gibbs force, compare affinity of reaction),
Eq. 4: ΔtrFX = ∂G/∂trξX [J·mol-1]
- Note that ∂G ≝ dtrG. Then inserting Eq. 2 and Eq. 3 into Eq. 4, the force of transformation is expressed as
Eq. 5: ΔtrFX = (µA·dtrnA + µB·dtrnB)/dtrξi [J·mol-1]
- Using Eq. 3, Eq. 5 can be rewritten as
Eq. 6: ΔtrFX = µA·dtrnA/(dtrnA·νA-1) + µB·dtrnB/(dtrnB·νB-1) [J·mol-1]
- This yields the force as the sum of stoichiometric potentials, summarized in Figure 8.5 (Chapter 8; Gnaiger 2020 BEC MitoPathways),
Eq. 7: ΔtrFX = µA·νA + µB·νB [J·mol-1]
- In general,
Eq. 8: ΔtrFX = Σµi·νi = ΣFtri [J·mol-1]
- It may arouse curiosity, why the sign of difference Δ is used in the symbol, whereas the equation suggest a sum Σ in contrast to a difference. This is best explained by the fact that in various conventional contexts — such as the classical formulation of the pmF — the stoichiometric numbers (-1 and +1) are omitted, which yields a difference Δ as an equivalence,
Eq. 9: ΔtrFX ≡ µB - µA [J·mol-1]
- The conceptual importance of the stoichiometric numbers is emphasized by defining the term stoichiometric potential (Gnaiger 2020), analogous to combining dtrnA·νA-1 in the expression of advancement (Eq. 3; see Eqs. 7 and 8),
Eq. 10: Ftri = µi·νi [J·mol-1]
- To get acquainted with the meaning of subscripts such as 'tr' used above, consult »Abbreviation of iconic symbols.
References
- Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. Bioenerg Commun 2020.2. https://doi.org/10.26124/bec:2020-0002
Footnote 1
- The original Figure 8.5 shows ∂trξX = ∂trnX∙νX-1 instead of dtrξX = dtrnX∙νX-1. The formal inconsistency was pointed out by Marin Kuntic during the BEC tutorial-Living Communications: pmF to pmP (Schroecken 2022 Sep 30-Oct 03).
- »Bioblast links: Energy and exergy - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Units
- Joule [J]; 1 J = 1 N·m = 1 V·C; 1 cal = 4.184 J
- Units
- Fundamental relationships
- » Energy
- » Exergy
- » Extensive quantity
- Fundamental relationships
- Contrast
- » Force
- » Pressure
- » Intensive quantity
- Contrast
- Forms of energy
- » Internal-energy dU
- » Enthalpy dH
- » Heat deQ
- » Bound energy dB
- Forms of energy
- Forms of exergy
- » Helmholtz energy dA
- » Gibbs energy dG
- » Work deW
- » Dissipated energy diD
- Forms of exergy
MitoPedia concepts:
Ergodynamics
